Recently, a research group led by Prof. Yong-Chun Liu from Department of Physics, Tsinghua University have used feedback to construct a parity-time symmetric Hamiltonian in a single dissipative resonant system, and effectively narrowed the linewidth of the system in the parity-time symmetric phase. The research results were published in Physical Review Letters under the title of "PT-Symmetric Feedback Induced Linewidth Narrowing".

Linewidth is one of the key factors that determine the performance of resonance systems, such as atoms, optical cavities and mechanical resonators. Especially, for precision measurement and sensing, we always strive for a narrow linewidth to achieve better measurement sensitivity. In various precision experiments such as atomic magnetometry and atomic gyroscopy, a very narrow linewidth enables to detect extremely weak signals. On the other hand, narrow linewidth also represents long coherence time, which is beneficial for quantum storage and quantum information processing. In order to reduce the linewidth, various methods have been proposed, e.g., anti-relaxation coating of vessel walls, spin-exchange-relaxation-free mechanism, nonlinear magneto-optical rotation approach and coherent population trapping scheme in atomic systems. However, these methods typically have specific and stringent requirements, e.g., highly demanding fabrication, strict magnetic shielding or specific energy levels. Therefore, a method for narrowing linewidths that is universally applicable to dissipative resonance systems and can be implemented using a simple device is of great significance.

They realized a novel type of parity-time-symmetric (PT-symmetric) system by utilizing a single resonance mode, which leads to efficient and tunable linewidth narrowing. In recent years, PT symmetry has attracted much interest, inspired by its unique property that exhibiting real energy spectra with non-Hermitian. The study of PT symmetry provides a powerful tool of engineering gain and loss and controlling the system linewidth. However, previous realizations of PT symmetry require two or more modes, which is not applicable in a large variety of systems which contain only a single resonance mode. They found that a single resonance system has two orthogonal quadrature. By constructing a quadrature measurement-feedback loop in which one quadrature component is measured with feedback [Fig1. (b)], an equivalent gain is introduced, breaking the symmetry between the quadratures and realizing a PT-symmetric system. By adjusting the feedback factor, the eigenvalues of the system can be controlled [Fig. 1(d)-(e)]. In the PT symmetric phase (orange area), the imaginary parts (dissipation) of the system's eigenvalues decrease with the increase of the feedback factor, resulting in a narrowing of the linewidth.

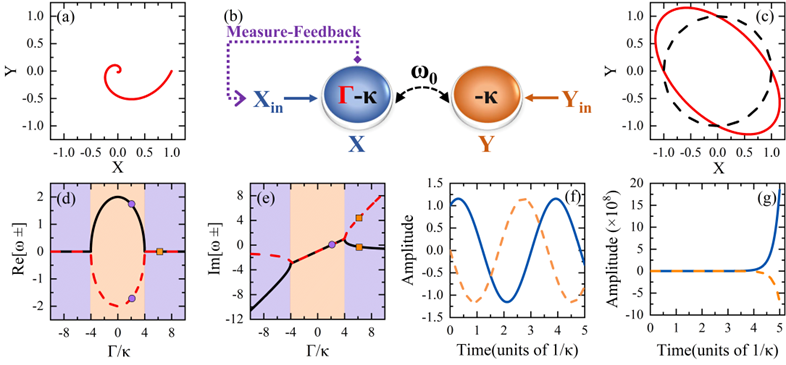
FIG. 1. (a) Typical trajectory of a dissipative resonance system in the phase space. (b) Schematic diagram of the PT -symmetric feedback system. (c) Phase-space trajectory of the PT -symmetric feedback system (red solid curve) and Hermitian resonance system (black dashed curve). (d),(e) Real and imaginary parts of the eigenvalues. (f),(g) Typical time evolution of quadratures X (blue solid curve) and Y (orange dashed curve) in PT -symmetric phase and symmetry broken phase.

They demonstrated the PT-symmetric feedback mechanism in a thermal atomic ensemble, which is a typical example of magnetic resonance system. A beam of circularly polarized laser propagating along the −z direction optically pumps the atomic ensemble to polarize the collective spin. A static magnetic field is applied along z axis, then the collective spin undergoes a Larmor precession around z axis. Thus the transverse components Px,y oscillates in the xy plane, constituting a harmonic oscillator. They measured the spin polarization component Px using a probe laser via polarization homodyne detection, and the output signal is then fed into a loop that includes a feedback resistor and the y-axis feedback coil, which generate the feedback magnetic field. The effect is that the gain is introduced into the Px orthogonal quadrature, breaking the symmetry of Px and Py, making the collective spin oscillator become a PT-symmetric system.

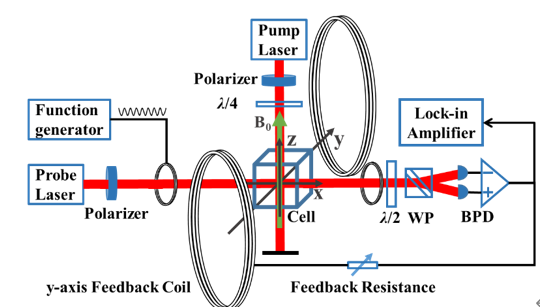
Fig.2. Experimental setup with a thermal atomic ensemble.

In the PT-symmetric phase, the feedback factor is controlled by the feedback resistance, which can conveniently adjust the linewidth of the system. The linewidth is reduced from 654 Hz to 13.6 Hz, which is 48-fold narrowing. By applying the method in magnetometry, they realized 22-times improvement of the measurement sensitivity. This work opens the avenue for studying non-Hermitian physics and high-precision measurements in resonance systems with feedback.

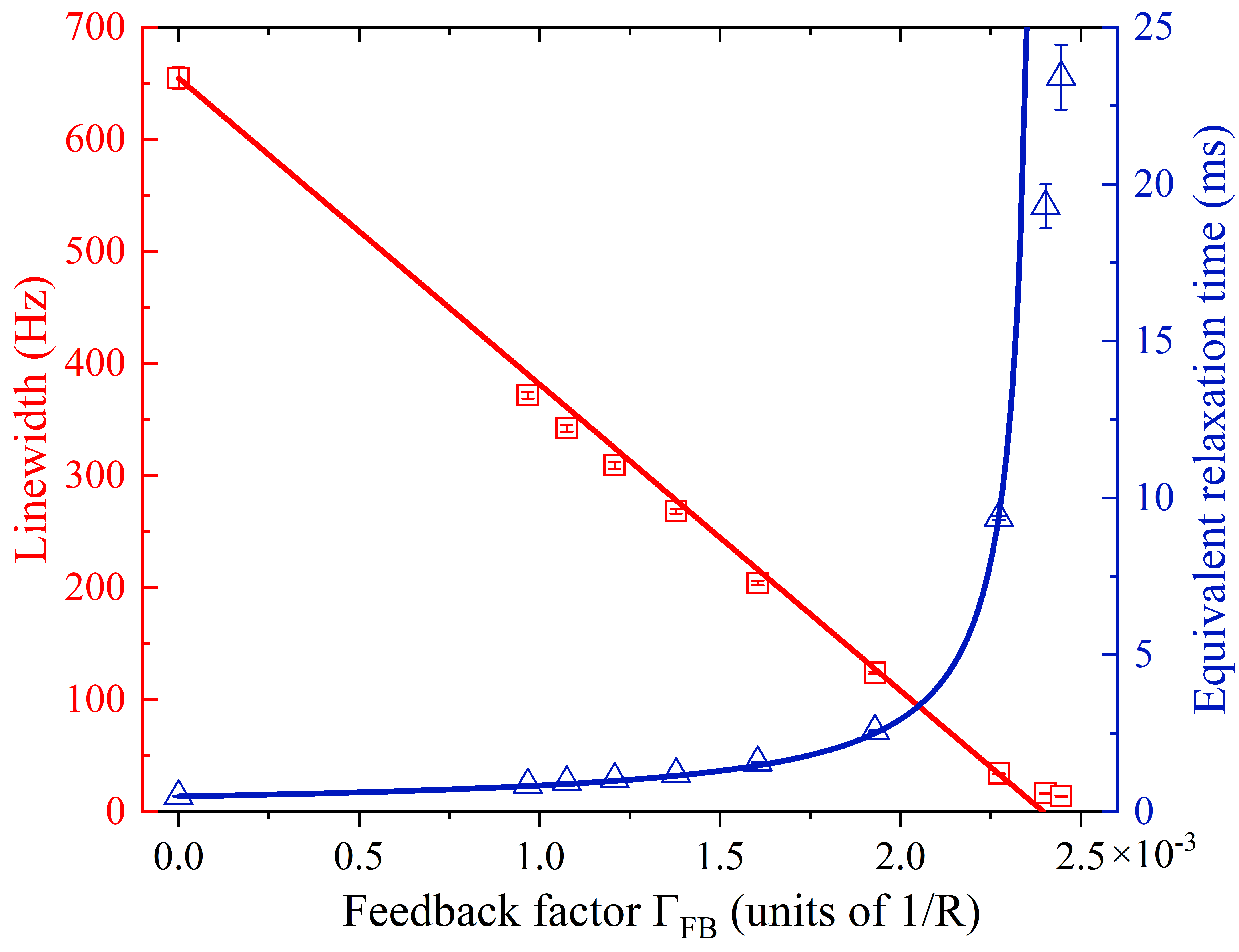
Fig.3. Dependence of linewidth and equivalent relaxation time on the feedback factor.

Research link: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.130.193602

Editor: Li Han